Replacing natural sand by crushed rock in concrete using nonlinear modelling
There is a lot of pressure to stop using natural sand and instead use crushed rock or recycled aggregate in concretes. However, crushed rock tends to have sharp corners, which affect not only the rheology of fresh concrete, but they also affect the strength of hardened concrete. So in this work, nonlinear models of a few properties of mortar were developed from experimental data.
There is a lot of pressure to stop using natural sand and instead use crushed rock or recycled aggregate in concretes. However, crushed rock tends to have sharp corners, which affect not only the rheology of fresh concrete, but they also affect the strength of hardened concrete. So it is not possible to add large amounts of crushed rock easily. To be able to determine recipes, which satisfy the specifications of fresh and hardened concrete, we need to know how the composition of the recipe affects the variables of those specifications.
As we have seen in very many cases, the effects are generally nonlinear. There are also cross term effects of pairs of variables. Linear statistical techniques are therefore not very suitable to describe those relations. Nonlinear models have been shown in many cases to be very efficient at describing those relations from a limited number of experiments. So in this work, nonlinear models of a few properties of mortar were developed from experimental data. Using those models, now we can calculate the largest fraction of crushed rock that can be added without compromising on the properties.
1 Introduction
Environmental considerations cause pressure on concrete producers to reduce their use of natural sand. The availability of sand is also reducing and in many countries, authorities have put restrictions on the use of natural sand. Crushed rock and waste aggregate tend to have less rounded edges and corners resulting in poorer flow of fresh mortar. A proper rheology is imperative for grouts and self-compacting concretes, and this limits the amount of crushed rock that can be used instead of natural sand, which tends to be more round.
A small fraction of crushed rock can be added without much experimentation, but to determine the maximum fraction of crushed rock, we need more precise knowledge on how it will affect the properties of fresh and hardened mortar. This is essentially a materials development problem, and the same approach, which has been used for various materials, can be utilized for mortars as well.
2 Materials development
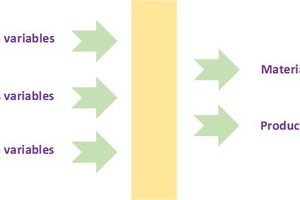
Materials development usually aims at achieving a set of desired material properties. However, it cannot be achieved at unreasonable costs. Production costs may include several variables like raw material cost, energy costs, labour costs per unit weight or unit volume, or total production cost per unit weight or unit volume, which should be affordable. All these variables depend on composition variables, or different amounts of materials fed into the process, the process variables by which the raw materials are processed, and dimension variables like particle size information, thicknesses, diameters, angles, or roundness of particles. The relations between the material properties and the variables on the left of Figure 2 are usually not very simple or linear.
To describe the relations of material properties with the variables on the left, physical modelling is hardly an option. Empirical or semi-empirical modelling is therefore used. Conventional empirical modelling is done using linear statistical techniques, which are not very good at describing nonlinearities. Nonlinear modelling, however, has shown to work effectively for a variety of materials. Readers of this magazine may recall the article from 2015 on self-compacting concrete [1] showing how nonlinear models helped drastically reduce production costs in the plant in Nummela in Finland.
3 Mathematical modelling with different
approaches
Mathematical models are quantitative descriptions in terms of variables. In other words, they contain concise knowledge of a system about the quantitative effects of selected variables. Such models try to emulate reality and can be used instead of experimentation, if they are of a sufficiently good quality. Mathematical modelling is performed with several different approaches.
Physical models are developed by writing laws of nature in a mathematical form. These models usually require plenty of assumptions and simplifications. It takes a lot of time to solve these equations, making them impractical for determining good values of process variables.
Empirical and semi-empirical modelling describe the reality as observed without the need of any major assumptions or simplifications. It requires observations either from production data, or from experiments. Empirical modelling is usually carried out with linear statistical techniques, which are not very efficient at describing nonlinearities in the effects of variables. Nothing in nature is very linear, and hence it makes sense to take nonlinearities into account by using the new techniques of nonlinear modelling.
4 Nonlinear modelling
One of the main purposes of this article is to improve the awareness about nonlinear modelling in the concrete and mortar industry. Nonlinear modelling is empirical or semi-empirical modelling which takes at least some nonlinearities into account. The older techniques include polynomial regression, linear regression with nonlinear terms, and nonlinear regression. These techniques have several limitations unlike the new techniques of nonlinear modelling based on free-form nonlinearities.
The new techniques of nonlinear modelling, particularly feed-forward neural networks, have turned out to be valuable in modelling processes and material behavior [2, 3] primarily because of their universal approximation capability [4]. It is usually possible to produce nonlinear models with some extrapolation capabilities with feed-forward neural networks. Artificial neural networks consist of neurons or nodes, usually arranged in layers and directionally connected to others in the adjacent layers. The multilayer perceptron (Figure 3) is a kind of a feed-forward neural network.
Nonlinear modelling has been successfully used in several industrial sectors including cement [5], concrete [6], glass [7], ceramics [8], metals [9], plastics [10], composites [11], rubbers [12], power generation [13], biotechnology [14], semiconductors [15] and medical materials [16].
Contrary to the common belief that neural networks need huge amounts of data, the truth is that they need fewer experiments if planned keeping in mind that the effects may be nonlinear, compared to conventional methods of experiment planning based on linear statistical techniques. Nonlinear models will tend to be more robust if they have been developed carefully. The models developed for this work ensured, for example, that the properties cannot be negative. Linear regression models would easily predict negative values.
5 Experimental data
Experimental or production data is needed to develop nonlinear models. During this work, an experimental approach was preferred. A total of 22 experiments were carried out with different crushed rocks with different particle sizes and roundnesses, and with different fractions of crushed rock. The data was first preprocessed and analyzed. Note that we have used Wadell’s function [17] of roundness instead of sphericity defined by the volume-area ratio because in the past, it has been noticed that roundness correlates better with the flow characteristics. Roundness was defined by Wadell [17] as the ratio of the average radius of curvature of the corners of the particle to the radius of the largest inscribed circle.
where n is the number of corners, ri the radius of the ith corner curvature, and rmax is the radius of the largest inscribed circle. Roundness would be exactly 1 for a perfect sphere and less than 1 otherwise.
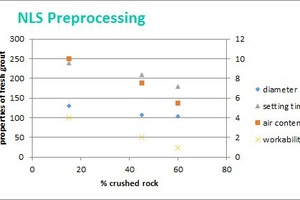
From the raw experimental data, some clear observations could be made. For example, increasing the fraction of crushed rock leads to lower flow table diameter, lower setting time, less air content and worse workability, as can be expected. It is seen from three experiments, data from which is plotted in Figure 4. It was not easy to carry out a series of experiments with different first decile diameters but with other variables constant. However, from the full set of data, it was visible that the overall effect of increasing the first decile diameter of crushed rock was smaller flow table spread, lesser air content, lower setting time, poorer workability but higher strengths at 7 days and 28 days.
6 Nonlinear models of six properties
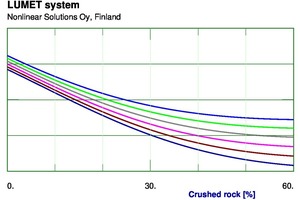
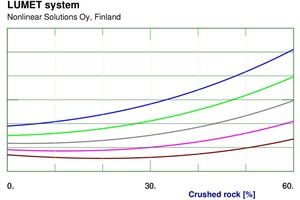
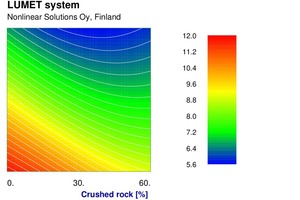
Nonlinear models were then developed using NLS 020 software. A large number of models were attempted with different configurations of neural networks with limitations on one or more weights in the networks. The finally selected models were then implemented in a Lumet system, a set of software components meant for facile use of the nonlinear models. The system has facilities for various kinds of calculations from the nonlinear models. It allows us to plot the effects of the input variables in a few different ways. Figure 5 depicts a series of curves for different values of the first decile diameter of crushed rock showing the effect of fraction of crushed rock on flow table spread. Similarly, Figure 6 shows the effect of fraction of crushed rock on compressive strength at 7 days for different values of roundness of crushed rock. Needless to say, the effects are not very linear, and linear statistical techniques are not very effective for describing these.
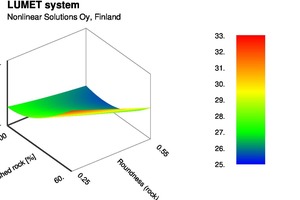
Figure 7 shows a contour plot of air content on a plane of fraction of crushed rock and first decile diameter of natural sand. To keep air content in an acceptable range, the feasible region is limited. The lower the D10 of sand, the more the crushed rock can be added. Figure 8 shows a surface plot of compressive strength at 28 days against fraction of crushed rock and roundness of crushed rock. Not only is the effect nonlinear, there is a strong cross term effect of this pair of variables. But now that we have the quantitative knowledge of the effects of the input variables on fresh and hardened mortar properties in the form of equations, it is easy to determine the maximum amount of crushed rock that can be used instead of natural sand and still have the properties within acceptable limits.
7 Conclusions
A good fraction of crushed rock or recycled aggregate can be used in place of natural sand without compromising on properties of fresh and hardened mortar. The largest fraction of crushed rock which can be added depends on the particle size distributions of natural sand as well as crushed rock, and also their roundnesses.
Nonlinear models to relate the properties of fresh and hardened mortar with the fraction of crushed rock, particle size distributions and roundnesses were developed from a fairly small series of experiments in a laboratory. There are strong nonlinear effects of some variables on the properties, and linear statistical techniques would not have been efficient. A simple software tool was created for use by Saint Gobain Weber which allows them to determine the maximum amount of crushed rock which can replace natural sand. The nonlinear models can be improved over time as more data is collected from different sands and aggregates.